Sine definition, a fundamental concept in trigonometry, unveils the mathematical intricacies of angles and their relationship to triangles. It serves as the cornerstone for a wide array of applications in engineering, physics, music, and beyond.

Delving deeper, we explore the sine function’s graph, highlighting its key features and characteristics. We delve into the inverse sine function, examining its connection to the sine function and its practical applications. Furthermore, we trace the historical development of sine, uncovering its origins and milestones.

Sine Definition

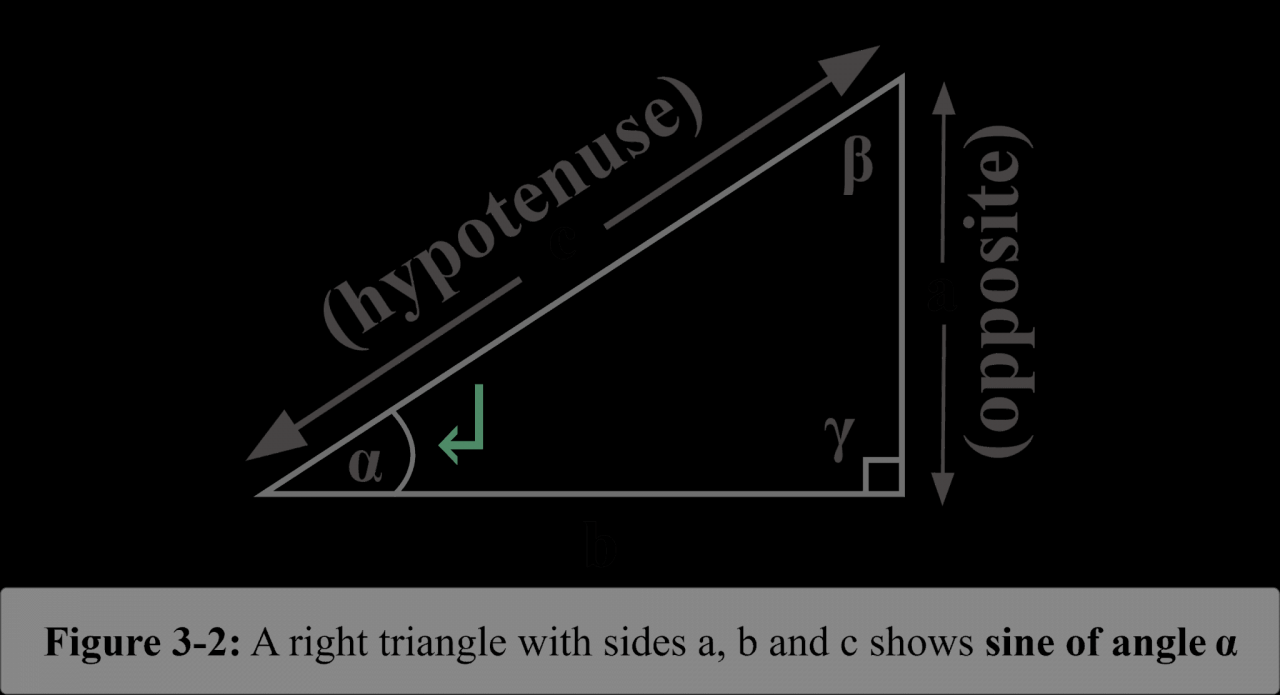
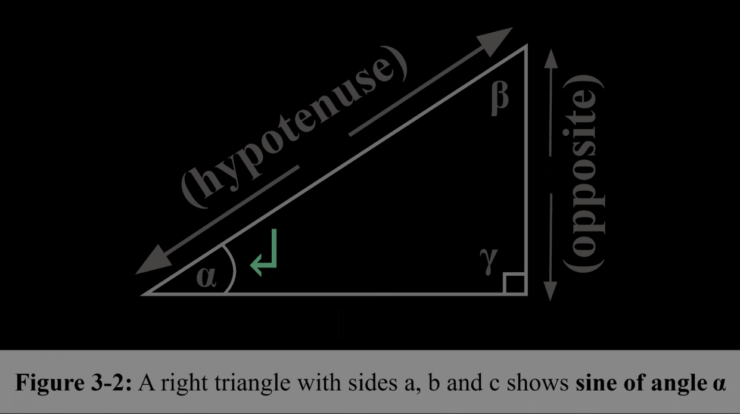
In mathematics, the sine function is a trigonometric function that relates the angle of a right triangle to the ratio of the length of the opposite side to the length of the hypotenuse.

Mathematically, the sine of an angle θ is defined as the ratio of the length of the opposite side (the side opposite the angle) to the length of the hypotenuse (the longest side) in a right triangle:

sin(θ) = opposite / hypotenuse

For example, in a right triangle with an angle of 30 degrees, the sine of that angle is 0.5, because the opposite side is half the length of the hypotenuse.

Applications of Sine

The sine function has numerous practical applications in various fields:

• Engineering:Sine is used to calculate distances, angles, and forces in structural design and analysis.
• Physics:Sine is used to model wave properties, such as amplitude and frequency, in areas like acoustics and optics.
• Music:Sine waves are used to create musical notes and tones in electronic music and sound synthesis.

Sine Function Graph

The graph of the sine function is a periodic curve that oscillates between -1 and 1.

• Amplitude:The maximum and minimum values of the sine function are 1 and -1, respectively.
• Period:The sine function repeats itself every 2π radians or 360 degrees.
• Phase Shift:The sine function can be shifted horizontally by adding a constant to the angle.

Inverse Sine Function

The inverse sine function (arcsine) is the inverse of the sine function.

It returns the angle that produces a given sine value:

arcsin(x) = θ such that sin(θ) = x

The arcsine function is used in applications such as navigation, signal processing, and computer graphics.

Relationship with Other Trigonometric Functions

Sine is closely related to other trigonometric functions, such as cosine and tangent.

The following identities hold true for all angles θ:

• cos(θ) = sin(90° – θ)
• tan(θ) = sin(θ) / cos(θ)

Historical Development, Sine definition

The concept of sine has been known since ancient times.

The first recorded use of the sine function was in the 2nd century AD by the Greek astronomer Claudius Ptolemy in his work “Almagest.”

The modern definition of the sine function was developed by Leonhard Euler in the 18th century.

Final Thoughts: Sine Definition

In essence, sine definition provides a powerful tool for understanding the world around us. Its applications span a vast spectrum of disciplines, enabling us to navigate, measure, and analyze complex phenomena. As we continue to explore the depths of trigonometry, the sine function remains a cornerstone, offering a gateway to unlocking the secrets of angles and triangles.

Commonly Asked Questions

What is the mathematical definition of sine?

Sine is defined as the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse.

How is sine used in engineering?

Sine is used in engineering to calculate distances, angles, and forces in structures, machines, and other systems.

What is the relationship between sine and other trigonometric functions?

Sine is related to other trigonometric functions, such as cosine and tangent, through trigonometric identities and formulas.